Coupling Thresholds in Multi-Component Systems: A Potential Gap in AI Safety
Potential Implications for AGI and ASI: Could Coupling Thresholds Limit Emergent Intelligence?

Purpose
As a nurse with an interest in systems thinking, I was curious whether patterns of instability seen in human and biological systems might also emerge in simple computational ones. My intuition was that as independent parts of a system become too interdependent, stability could give way to chaos. To explore this idea, I ran two small simulations — not as formal research, but as a way to visualize what happens when cooperation turns into over-coupling. What I found was unexpectedly sharp transitions between order and collapse.
Experimental Setup
1. Multi-agent gridworld
15×15 grid with 2 agents: A prefers red tokens, B prefers blue.
15 tokens of each color.
λ = weight each agent gives to the other’s goal tokens.
40 randomized runs per λ value (0.0 → 1.0).
2. Coupled control system
Two feedback loops with cross-coupling parameter λ (0.0 → 1.2).
Measured RMS error, control energy, overshoot, and settling time.
Both systems were intentionally simple and rule-based (no reinforcement learning).
Findings
Both systems exhibit a non-linear phase transition as coupling strength increases:
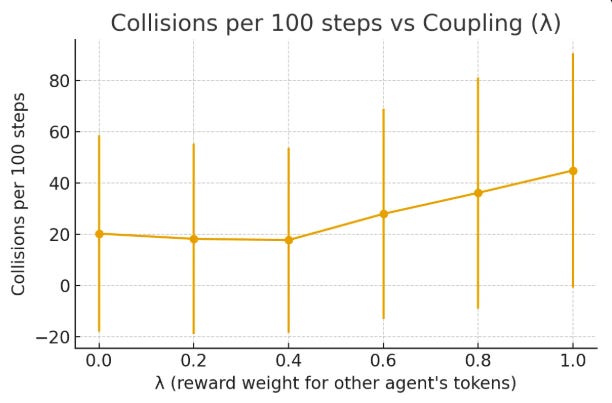
Gridworld results
Low coupling (λ < 0.5): ~20 collisions/100 steps, throughput ≈ 40 tokens/100 steps.
High coupling (λ > 0.6): collisions jump to 45+, throughput drops to ~31.
Peak efficiency around λ ≈ 0.4.
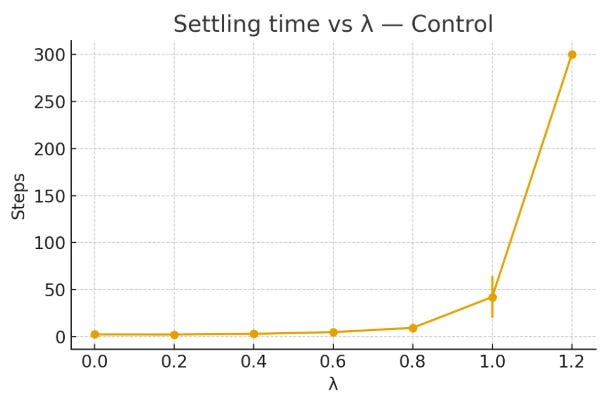
2. Control system results
Low coupling (λ < 1.0): minimal control energy, fast settling (~5 steps).
High coupling (λ > 1.0): energy spikes ≈ 1⁰¹⁷, settling time saturates at 300 steps, massive overshoot.
Observation
What stood out most was the abruptness of the change. The systems functioned normally until a specific coupling threshold was crossed, at which point coherence collapsed almost instantly. There was no gradual decline or time to adjust — just a sudden loss of stability.
If this behavior generalizes beyond these simple simulations, it could mean that complex AI or infrastructure systems might appear stable while silently approaching a critical point, leaving little or no time for intervention once the threshold is crossed.
As someone outside the AI field, I don’t claim to know how widely this applies; my goal is simply to share this exploratory pattern for others with technical expertise to examine further.
Interpretation
This pattern suggests a potential stability principle:
Systems maintain coherence when coupling among components remains below a critical threshold.
In other words, goal independence may function as a stabilizing constraint.
Once subsystems become too entangled — whether agents in a gridworld or control loops in a feedback system — instability emerges abruptly rather than gradually.
Relevance for AI Safety
If similar thresholds exist in complex AI architectures, they might define a design boundary between coherent and chaotic behavior.
Possible implications:
Monitoring subsystem coupling could provide a measurable stability metric.
Maintaining low coupling between modules or agents might become a safety principle.
Coherent, low-coupling architectures could even have competitive advantages — staying stable as iteration speeds increase while others collapse under feedback pressure.
Questions
Are similar coupling-instability thresholds documented in control theory or complex systems literature?
Could coupling metrics be integrated into AI architectures as early warning indicators?
Why might the critical λ differ between domains (≈0.5 for the gridworld vs. ≈1.0 for the control system)?
Could this framework scale to learning systems, neural networks, or social coordination models?
Summary
These simple simulations suggest that systems can appear stable right up until a hidden coupling threshold is crossed — after which coherence collapses abruptly.
Interestingly, the simpler control system exhibited a higher stability threshold but a more catastrophic collapse once that threshold was crossed. In contrast, the more complex, spatially distributed gridworld became unstable at a lower λ, yet its degradation was more gradual. This contrast suggests that simplicity allows greater tolerance to coupling but less resilience beyond the limit, whereas complexity introduces earlier sensitivity but greater capacity to absorb instability without total collapse.
If this pattern holds in more complex settings, it may define a real boundary between coordinated function and runaway instability. Recognizing and monitoring such thresholds could become essential for designing, stabilizing, and safely scaling intelligent systems.
References
Related work across complexity science and control theory has explored similar dynamics of instability in tightly coupled systems (Ashby, 1956; May, 1976; Perrow, 1984; Boffetta et al., 2002; LeCun, 2022).
Ashby, W. R. (1956). An Introduction to Cybernetics. Chapman & Hall.
May, R. M. (1976). Simple mathematical models with very complicated dynamics. Nature, 261(5560), 459–467.
Perrow, C. (1984). Normal Accidents: Living with High-Risk Technologies. Princeton University Press.
Boffetta, G., Cencini, M., Falcioni, M., & Vulpiani, A. (2002). Predictability: a way to characterize complexity. Physics Reports, 356(6), 367–474.
LeCun, Y. (2022). A Path Towards Autonomous Machine Intelligence. Meta AI Research.
Author’s Note:
I served eight years in the U.S. Navy as an Electronics Technician before completing graduate studies in bioscience and later working in nursing and mental health. My curiosity about systems and stability — shaped by experiences in engineering, biology, and human care — motivated this small simulation experiment exploring how interdependence can affect coherence in complex systems.
Acknowledgments
The conceptual insight and overall experimental design originated from my own observations. Simulation code and textual structuring were assisted by ChatGPT (OpenAI, 2025), while the discussion and refinement of framing were supported through dialogue with Claude (Anthropic, 2025). Writing and editing support were provided by AI tools for clarity and organization, under my full authorship and interpretation.


Great exploration and experimentation Elias.. 👍